The Discrete Element Method (DEM) is a numerical technique used in granular mechanics in which solid particles are treated as a system of interacting particles using the theoretical basis of Newton’s laws of motion. These interactions are coupled forces acting on a pair of individual particles and their subsequent positions, velocities, and accelerations over time.
Basic Principles
In DEM, finite particle collisions and rotations dominate the contact forces. The total contact force is a summation of the mechanical contact and body forces, such as gravity, magnetic, electrostatic, fluid drag, or cohesion/adhesion. A time integration scheme is used to approximate each particle’s location, linear/angular velocities and accelerations.
Many mathematical models have been proposed to approximate the physical behavior of the true interactions. One of the most common is a soft contact approach. It intends to model the deformation of the interacting bodies at a contact point by treating the particles as rigid bodies and the interactions between them governed by the unilateral contact, energy dissipation by friction and inelastic collisions.
Material Properties
Energy dissipation by friction and inelastic collisions are modeled by spring-dashpot elements. The spring stiffness is a function of the material size and properties such as the Young’s Modulus, and Poisson’s Ratio. Quantifying the energy loss is lumped with the damping effects related to the coefficient of restitution.
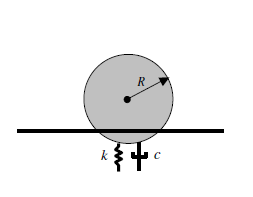
is the relationship between the damping of the system relative to critical damping
is the natural frequency of simple harmonic oscillation
can be described by
and