The yield strength of the macro-scale cohesion of particulate materials can be described by Coulomb cohesion. The Mohr-Coulomb failure criterion, described by:
divides the mechanical strength of the material into the angle of internal friction and the macroscopic cohesion of the material c [1]. Here and
are the normal and tangential stresses. These parameters characterize the material at particular stress states and can extend the effects of cohesion into the elastic domain in the stress plane. The angle of internal friction and the macroscopic cohesion can be determined with physical tests of shear, compression or tension. Particulate materials are typically tested under compressive loading. Under a uniaxial compression test, the yield strength
of the material can be derived by:
The figure provides a graphical representation of Mohr-Coulomb’s criterion where the parameters and c characterize the strength of the material. The straight line represents the linear failure envelope that is obtained from the shear strength of a material at a particular state of stress in the material.
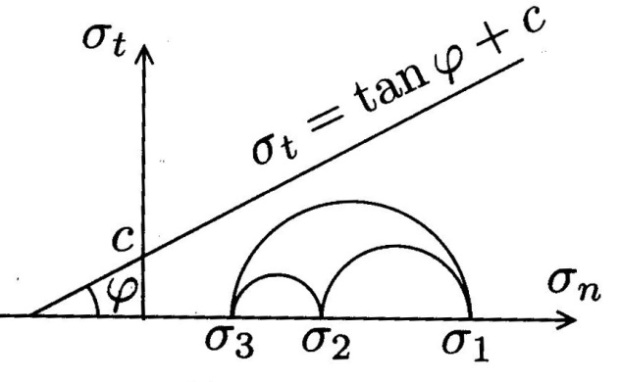
Morh-Coulomb Criterion [2].
- Nedderman R. M., Statics and Kinematics of Granular Materials, Cambridge Univeristy Press, Cambridge, 1992.
- Farhang R., Dubois F., Discrete-Element Modeling of Granular Materials, John Wiley & Sons Inc. 2011