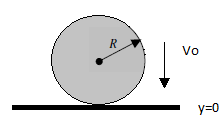
Condition 1: At time = 0 and position y = 0
Therefore: A = 0
To use the condition of at t = 0, we need to take the first derivative of the position equation
This brings our position and velocity equations to:
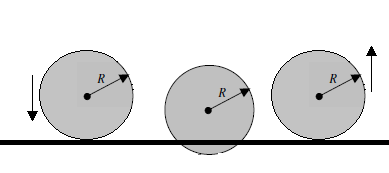
The goal of solving this system is to extract the damping coefficient. To do this, evaluate the system at the instant the particle rebounds from the ground.
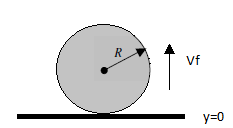
These conditions are: y = 0, ,
First we need to determine
The equation for position is a sine wave of the form:

The sine wave has a period T and the time elapsed during that period is T/2, where
period,
Therefore,
time,
Solving the velocity equation at the determined conditions: ,
Using this information for and
combined with the linear definition of the coefficient of restitution, e, which is given by:
Bringing out system to its initial terms: m, k, c
Recall:
damping ratio,
This defines the viscous damping coefficient.