Deriving the Damping Coefficient (part 1)

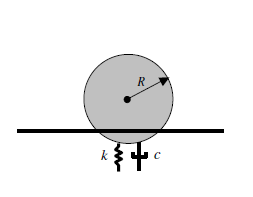
damp1

$m\ddot{y}\ + c\dot{y}\ + ky\ = 0$ $y\leq 0$

This differential equation can be re-arragned as

$\ddot{y}\ + \frac{c}{m}\dot{y}\ + \frac{k}{m}y\ = 0$ $y\leq 0$

$\ddot{y}\ + \ 2 \zeta \omega_0 \dot{y}\ + \omega_0^2\ y= 0$ $y\leq 0$

Where $\zeta$ is the relationship between the damping of the system relative to critical damping $\omega_0$ is the natural frequency of simple harmonic oscillation

critical damping coefficient, $C_{crit}\ = 2 \sqrt{km}$

damping ratio, $\zeta = \frac{c}{C_{crit}} \rightarrow \frac{c}{2 \sqrt{km}}$

natural frequency, $\omega_0 = \sqrt{\frac{k}{m}}$

Therefore, $\frac{c}{m}$ can be described by $2 \zeta \omega_0$

$2 \zeta \omega_0 = 2\frac{c}{2 \sqrt{km}} \sqrt{\frac{k}{m}}$

$2 \zeta \omega_0 = \frac{c}{\sqrt{k} \sqrt{m}} \frac{\sqrt{k}}{\sqrt{m}}$

$2 \zeta \omega_0 = \frac{c}{\sqrt{m} \sqrt{m}} \ = \frac{c}{m}$

Solving for the general solution to this system, $\ddot{y}\ + \ 2 \zeta \omega_0 \dot{y}\ + \omega_0^2\ y= 0$ $y\leq 0$

Start by identifying the roots of the system and obtaining the general solution.

Roots of the auxiliary equation

$r^2\ + \ 2 \zeta \omega_0 r \ + \omega_0^2 = 0$

$r = \frac{-2 \zeta \omega_0 \pm \sqrt{(2 \zeta \omega_0)^2 - 4 \omega_0^2}}{2}$

$r = \frac{-2 \zeta \omega_0}{2} \pm \frac{1}{2} \sqrt{4 \zeta ^2 \omega_0^2 - 4 \omega_0^2}$

$r = - \zeta \omega_0 \pm \sqrt{ \zeta ^2 \omega_0^2 - \omega_0^2} \rightarrow \ -\zeta \omega_0 \pm \sqrt{-1} \sqrt{ \omega_0^2 - \zeta ^2 \omega_0^2}$